Question

find an equation of the line containing the two given points.Express your answer in the indicated form. points (1,2) and (3,10):standard form

Answer 1

Equation of the line

There are several forms to express the equation of a line.

The equation of the line in slope-intercept form is:

y=mx+b

Being m the slope and b the y-intercept.

The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

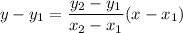
The standard form of a line is:

Ax + By = C

We are given two points (1,2) and (3,10). The point-point equation is adequate according to the data we are provided.

`\begin{gathered} \displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ \text{Substituting:} \\ \displaystyle y-2=(10-2)/(3-1)(x-1) \end{gathered}`

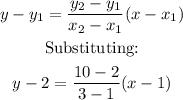
Operating:

`\begin{gathered} y-2=(8)/(2)(x-1)=4(x-1) \\ \\ \text{Operating:} \\ y-2=4x-4 \end{gathered}`

Subtracting 4x and adding 2:

y - 4x = -4 + 2 = -2

Rearranging:

-4x + y = -2

This is the required equation in standard form