Question

Solve the inequality. Write the solution set in interval notation.9−xx+11≥0Select one:a. [-11, 9)b. (-∞, -11] U [9, ∞)c. (-∞, -11) U (9, ∞)d. (-11, 9]

Answer 1

We need to solve the following inequality:

`(9-x)/(x+11)\ge0`

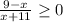
Then we have that for the inequality would be complied we have two implicit conditions:

`9-x\text{ }\ge\text{ 0}`

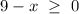
And at the same time:

`x+11>0`

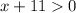
You have to be careful because we already know that the denominator of a fraction can not be zero, it's, for this reason, the second inequality.

But, in a second case, we can also have both numerator and denominator as negative numbers, it also gives us a number bigger or equal to zero.

So we have the inequalities:

`9-x\leq0`

And:

`x+11<0`

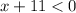
Firstly we can focus on the first case if we solve for x:

`9-x\ge0`
`x\leq9`

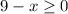
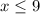
And the denominator inequality of this case:

`x+11>0`
`x>-11`

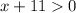
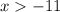
And how we must have the agreed interval between the conditions, we have that the first result for this case is the interval:

(-11,9], or in a equivalent form: -11

From the second case, when both numerator and denominator we have:

`9-x\leq0`
`x\ge9`

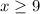
And from the denominator inequality:

`x+11<0`
`x<-11`

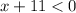
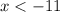
So a second result is an interval that doesn't exist because a number biggest of 9 and smallest than -11 doesn't exist in the real number.

Then we obtain the final result, and the correct answer is:

(-11,9], or in a equivalent form: -11

D.