Given the word problem, we can deduce the following information:
1. A triangular plot of land has angles 46° and 58°.
2. The side opposite the 46° is 35 m long.
To determine the length of the fence to enclose the entire plot of land, we make a figure of the triangular plot first:
where:
x= the third angle
a= side opposite of 58°
b= side opposite of x°
Since the sum of the interior angles of a triangle is 180°, we can get the value of x by:
x=180-46-58
x=76°
Next, we use the Law of Sines proportion as shown:
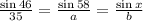
Then, we find the value of a:
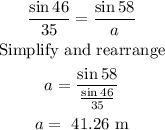
We also need to find the value of b:
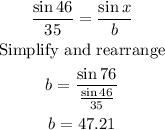
Hence, we add the sides of which rounded to the nearest meter to get the total length of the fence:
Fence = 35+41+47 =123 meters
Therefore, the length of the fence to enclose the entire plot of land is:
b. 123 meters