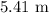Question

A 63.1 kg weight-watcher wishes to climb a mountain to work off the equivalent of a large piece of chocolate cake rated at 797 (food) Calories. How high must the person climb? The acceleration due to gravity is 9.8m/s^2 and 1 food Calorie is 10^3 calories. Answer in units of km.

Answer 1

Given:

the mass of the weight-watcher is

`m=63.1\text{ kg}`

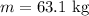
The work off equivalent to

`W=797\text{ food}`

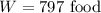
Required: height climbed by the person

Step-by-step explanation:

first we need to change the work into calories.

it is given that

`1\text{ food=10}^3\text{ calories}`

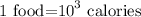
then the work done is

`W=797*10^3\text{ calories}`

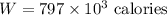
now change this work done from calories to joules.

we know that

`1\text{ calorie = 4.2 J}`

Then the work done is ,

`\begin{gathered} W=797*10^3*4.2 \\ W=3347.4*10^3\text{ J} \end{gathered}`

as the person climbs to the mountain the work done is stored as potential energy.

we assume that a person attained some height h,

then the work-energy relation,

`W=mgh`

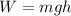
Plugging all the values in the above relation and solve for h, we get

`\begin{gathered} 3347.4*10^3\text{ J=63.1 kg}*9.8\text{ m/s}^2* h \\ h=(3347.4)/(618.38) \\ h=5.41\text{ m} \end{gathered}`

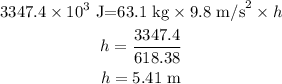
Thus, the height climbed by the person is

`5.4\text{1 m}`