Question

A triangle has two sides of length 13 and 7. What is the smallest possible whole-numberlength for the third side?

Answer 1

6

Step-by-step explanation

We want to find the smallest possible length of the third side.

To do this, we apply the Triangle Inequality Rule.

It states that the sum of the two sides of a triangle must be greater than or equal to the length of the third side.

Let the length of the third side of the triangle be x.

This could then mean 3 things:

`\begin{gathered} 13+7\ge x \\ 13+x\ge7 \\ x+7\ge13 \end{gathered}`

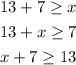
Now, we have to solve each of them to find the least possible value of x:

`\begin{gathered} \cdot20\ge x\Rightarrow x\le20 \\ \cdot x\ge7-13\Rightarrow x\ge-6 \\ \cdot x\ge13-7\Rightarrow x\ge6 \end{gathered}`

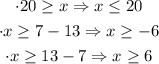
The first option cannot work because then we are dealing with the greatest possible value of x as 20.

The second option cannot work because x cannot be a negative value.

The third option is valid.

Therefore, the smallest possible value of the length of the third side of the triangle is 6.