Question

I need help with this story problem it very confusing can explain this step by step instructions so I understand. Huh, low battery again?! Samantha had just charged her phone up to 76%, and now it was already down to 16%. She had only streamed... oh... oops...three whole episodes of The Haunted Cave this morning (each episode is exactly thirty minutes). That afternoon, after having her phone plugged in for the past hour, she hopped on a bus to meet her friend Jorge at zoo. During the 24-minute ride, she listened to her favorite playlist, Top Pop, noticing her charge had only dropped from 63% to 59%. Not bad!At the edge of the monkey habitat, Samantha pulled out her phone to snap a photo. Suddenly, the monkeys started doing amazing flips and tricks. It was as if they were creating a distraction... "Wait! No!" One of those crafty monkeys swiped her phone right out of her hand! The other monkeys gathered around, guffawing, as the first monkey begin tapping the screen.When Samantha finally got her phone back, the monkey had drained the battery all the way to 31%, boo!On the bus home, Samantha turned on Top Pop to calm herself. " Too bad your battery's at 29% now. I'm still at 55%," Jorge said, while watching The Haunted Cave. Samantha eyed their phones thoughtfully.If Jorge's phone battery drains at the same rate as Samantha's, and they continue playing their current media, how many minutes will it be before the two phones have the same battery level?

Answer 1

When Samantha was streaming "The Haunted Cave" the cellphone went from a level of battery charge of 76% to 16%. We need to calculate the rate at which the battery of the phone is drained while streaming this show. She watched three episodes of the show, each with 30 minutes. So the first step is to calculate the time she spent streaming it. Since she watched 3 episodes of 30 minutes each, the total time is the product between the number of episodes and the elapsed time.

`\text{time}_{\text{haunted}}=3\cdot30=90\text{ minutes}`

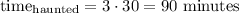
Then we need to calculate how much of the battery was spent on that time. This is the difference between the charge when she started and the charge when she finished.

`\text{charge}_{\text{dif}}=76-16=60\text{ \%}`

Now we can calculate the rate at which her battery is drained while watching that show, this is done by dividing the total battery spent by the elapsed time.

`\text{rate}_{\text{haunted}}=(60)/(90)=(2)/(3)\text{ \% per minute}`

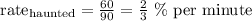
This rate means that for every minute watching this show she spends 2/3 of a % of battery.

She then charged the battery to 63% and went on a 24 minute bus ride while listening to Top Pop, this resulted on her battery dropping all the way to 59%. We need to do the same as above to find how much batter per minute this playlist consumes. We have:

`\text{charge}_{\text{dif}}=63-59=4\text{ \%}`

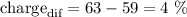
The playlist spent 4% in 24 minutes, so the rate is:

`\text{rate}_{\text{playtop}}=(4)/(24)=(1)/(6)\text{ \% per minute}`

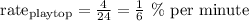
While listening to Top Pop the cellphone discharges at a rate of 1/6 of a % per minute.

When she was on the bus home with her friend her battery was at a level of 29%, while his was at 55%. He then went to watch the haunted show, while she went to listen Play Top. If the rate is the same as we calculated above, then the level of battery of each person can be calculated by the starting level subtracted by the rate at which each app consumes the battery multiplied by the time they are using the app. So for each person we have:

`\begin{gathered} \text{samantha}=29-(1)/(6)\cdot t \\ \text{jorge}=55-(2)/(3)\cdot t \end{gathered}`

To find the time it will take before the level of battery is the same on each device we need to make both equations equal and solve for t.

`\begin{gathered} 29-(1)/(6)\cdot t=55-(2)/(3)\cdot t \\ (2)/(3)t-(1)/(6)t=55-29 \\ (2\cdot2t-t)/(6)=26 \\ (4t-t)/(6)=26 \\ (3t)/(6)=26 \\ (t)/(3)=26 \\ t=26\cdot3=78\text{ minutes} \end{gathered}`

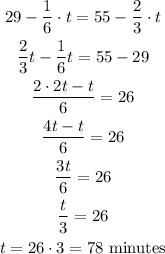
For both phones to achieve the same level of battery they'll need to use it for 78 minutes.