Solution:
The continuous compound interest formula is expressed as
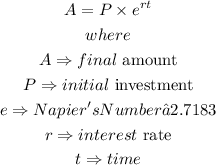
Given that $10 is invested at 10% compounded continuously after a period of 3 years, this implies that
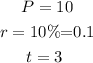
The amount that results from the investment is evaluated by substituting these above values into the equation.
Thus,
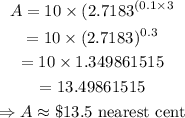
Hence, the amount that results from the investment is evaluated to be $13.5 (nearest cent).