Question

Question attached Answer 1 A. B>1B. 01F 01B. 01F. 0

Answer 1

Step-by-step explanation:

Given;

We are given the general form of an exponential function and that is;

`y=a* b^x`

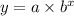
Required;

We are required to determine when it represents a growth and when it represents a decay.

Step-by-step solution/explanation;

The exponential function in its expanded form is given as follows;

`y=a(1+r)^x`

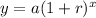
Take note of the following variables;

`\begin{gathered} a=initial\text{ }value \\ r=rate\text{ }of\text{ }growth \\ x=interval,\text{ }years,\text{ }days,\text{ }etc \end{gathered}`

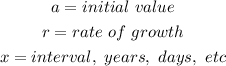
Hence, note also, that;

`(1+r)=growth\text{ }factor`

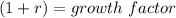
Note also that;

`(1+r)=b`

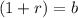
Therefore, if there is a growth, the formula would be;

`y=a(1+r)^x`

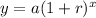
Which means;

`\begin{gathered} (1+r)>1 \\ OR \\ b>1 \end{gathered}`

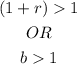
And if there is a decay, the formula would be;

`y=a(1-r)^x`

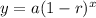
Which means;

`\begin{gathered} (1-r)<1 \\ OR \\ b<1 \end{gathered}`

Therefore,

ANSWER:

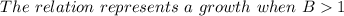
`The\text{ }relation\text{ }represents\text{ }a\text{ }growth\text{ }when\text{ }B>1`[tex]And\text{ }a\text{ }decay\text{ }when\text{ }0First is option A

Second is option B