Question

Given that sin A =3/5 and tan B= -12/5 where A is an acute angle and B is an obtuse angle. Without using tables or calculators, find the value of (a) tan A(b) cos (A+B)

Answer 1

The given angles are sin A =3/5 and tan B= -12/5 where A is an acute angle and B is an obtuse angle.

a. To determine tan A

First find the cos A with the help of trigonometric property

`\cos A=\sqrt[]{1-\sin ^2A}`
`\cos A=\sqrt[]{1-(9)/(25)}=(4)/(5)`
`\tan A=(\sin A)/(\cos A)=(3)/(4)`

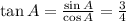
b. To determine cos(A+B)

`\cos (A+B)=\cos A\cos B-\sin A\text{ sin B}`

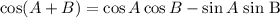
We have to find sin B and cosB, it is given that tan B= -12/5

`\sec ^2B=1+tan^2B`
`\sec ^2B=1+(144)/(25)=(169)/(25)`
`\sec B=(13)/(5)`

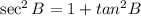
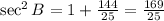
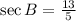
Then the value of cos B is 5/13.

Determine the value of sinB

`\sin B=\sqrt[]{1-(25)/(169)}=(12)/(13)`

The value of cos (A+B) i

​