Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar. The focus of a parabola is (0,-1). The directrix is the line y = 0. What is the equation of the parabola in vertex form? (-k)² + h, the value of p is - In the equation y The vertex of the parabola is the point ( The equation of this parabola in vertex form is y: = x² - 1

Answer 1

we know that

Focus (0,-1)

Directrix is the line y=0

so

we have a vertical parabola open downward

Remember that

The distance from the vertex to the directrix must be the same that the distance from the vertex to the focus

which means

The vertex is the point (0,-0.5) ----> midpoint between the focus and the directrix

Find out the value of p (focal distance)

p=0.5

The equation of the parabola is given by

`\begin{gathered} y=-(1)/(4(0.5))(x-0)^2-0.5 \\ \\ y=-(1)/(2)x^2-0.5 \end{gathered}`

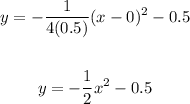
The vertex is (0,-0.5)

The value of p=0.5