Question

Find the equation of each line from the given information(a) through (2,2), slope =2 (b) through ( 5,6) and (2,1 ) (f) x-intercept 5, y-intercept -4(i) inclination 30º, x-intercept 5

Answer 1

a)

To determine the equation of a line knowing its slope and a point it passes trough you have to use the point-slope form:

`y-y_1=m(x-x_1)`

Where

m is the slope

(x₁, y₁) are the coordinates of the point of the line.

Replace the given values in the formula:

m=2 and point (2,2)

`y-2=2(x-2)`

You can write the equation in slope-intercept form:

1-distribute the multiplication on the parentheses term

`\begin{gathered} y-2=2x-2\cdot2 \\ y-2=2x-4 \end{gathered}`

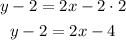
2-pass the number to the right side of the equation

`\begin{gathered} y-2+2=2x-4+2 \\ y=2x-2 \end{gathered}`

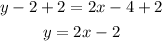
b)

For this item, the information known of the line are two points it passes through (5,6) and (2,1)

The first step is to determine the slope of the line, you can do so by applying the following formula:

`m=(y_1-y_2)/(x_1-x_2)`

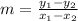
Where

m is the slope

(x₁, y₁) are the coordinates of one point on the line

(x₂,y₂) are the coordinates of a second point on the line

Using the coordinates of the given points, replace them in the formula

`\begin{gathered} m=(6-1)/(5-2) \\ m=(5)/(3) \end{gathered}`

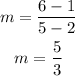
Now that we know the slope, we can use the point slope form to determine the equation of the line.

You can use either point to determine the equation, the final result is the same, I will use m=5/3 and point (5,6)

`y-y_1=m(x-x_1)`
`y-6=(5)/(3)(x-5)`

Solve the multiplication on the parentheses term

`\begin{gathered} y-6=(5)/(3)x-(5)/(3)\cdot5 \\ y-6=(5)/(3)x-(25)/(3) \end{gathered}`

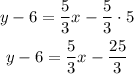
Pass "-6" to the other side of the equation to express it in slope-intercept form:

`\begin{gathered} y-6+6=(5)/(3)x-(25)/(3)+6 \\ y=(5)/(3)x-(7)/(3) \end{gathered}`

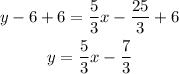
f) x-intercept 5, y-intercept -4

The x-intercept is the point where the line crosses the x-axis, at this point the y-coordinate is equal to zero. So the coordinates for the x-intercept for this line is (5,0)

The y-intercept is the point where the line crosses the y-axis, at this point the x-coordinate is equal to zero, then the coordinates for the y-intercept of this line is (0,-4)

Using the coordinates of both intercepts you can calculate the slope of the line:

`m=(y_1-y_2)/(x_1-x_2)`
`\begin{gathered} m=(0-(-4))/(5-0) \\ m=(4)/(5) \end{gathered}`

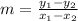
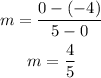
Once determined the slope of the line, use the point-slope form to determine the equation:

m=4/5 point (5,0)

`y-y_1=m(x-x_1)`
`\begin{gathered} y-0=(4)/(5)(x-5) \\ y=(4)/(5)x-5\cdot(4)/(5) \\ y=(4)/(5)x-4 \end{gathered}`

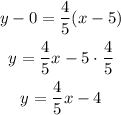
i) inclination 30º, x-intercept 5

In this case, we know the angle of inclination of the line. There is a relationship between the angle of inclination and the slope of the line and that is:

`m=\tan \theta`

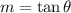
Where θ represents the angle of inclination.

The slope of a line is equal to the tangent of the angle of inclination.

For this example θ=30º, then the slope can be calculated as:

`\begin{gathered} m=\tan 30 \\ m=\frac{\sqrt[]{3}}{3} \end{gathered}`

The x-intercept of this line is 5, the coordinates for this point are (5,0)

Now that the slope of the line is determined, you can use the point-slope form to determine the equation:

`y-y_1=m(x-x_1)`
`\begin{gathered} y-0=\frac{\sqrt[]{3}}{3}(x-5) \\ y=\frac{\sqrt[]{3}}{3}x-5\cdot\frac{\sqrt[]{3}}{3} \\ y=\frac{\sqrt[]{3}}{3}x-\frac{5\sqrt[]{3}}{3} \\ y=0.58x-2.87 \end{gathered}`

Note:

Two lines are parallel when they have the same slope.

Two lines that are perpendicular, their slopes are opposite reciprocals.

The method to determine the equations of the lines is as followed above. Knowing at least one point of the line, you have to determine the slope of the line and then apply the point-slope form to determine its equation.