Question

Name the center and the radius of the(x + 1)2 + (y + 4)2 = 49O (center:(-1,-4) and radius: 7O center: (1,4) and radius: 7O center: (1, 4) and radius: 49O center:(-1,-4) and radius: 49

Answer 1

center: (-1, -4) and radius: 7

Step-by-step explanation:

The standard form of the equation of a circle is given as;

`(x-a)^2+(y-b)^2=r^2`

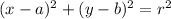
where (a, b) are the coordinates of the center and r is the radius.

Given the below equation of a circle in the question;

`(x+1)^2+(y+4)^2=49`

If we compare the given equation with the standard equation of a circle, we can see that a, b and r can be found as shown below;

For a;

`\begin{gathered} -a=1 \\ \therefore a=-1 \end{gathered}`

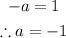
For b;

`\begin{gathered} -b=4 \\ b=-4 \end{gathered}`

For r;

`\begin{gathered} r^2=49 \\ r=\sqrt[]{49} \\ \therefore r=7 \end{gathered}`