Question

Find the range, standard deviation and the variance of 7,9,14,16,18,22,23Round non-integer results to the nearest tenth.

Answer 1

To answer this question, we need to know that the asked statistics, namely, the standard deviation and the variance, in this question are for a sample, and the formula for this is given as follows:

1. Sample Variance

`(Sx)^2=(1)/(n-1)\sum ^n_(i\mathop=1)(x_i-\bar{x})^2`

2. The standard deviation is the square root of the sample variance.

We have that:

• n = number of observations in the sample

,

• x (bar) is the mean of the data

,

• x_i are the values in the data

Now, we have that the data is: 7, 9, 14, 16, 18, 22, 23 (there are seven observations, n = 7).

Range

3. The range of the values is the result of the subtraction, the difference, between the largest observation and the smallest observation in the data. Then, we have that the range is:

`\text{Range}=23-7=16`

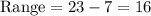
Now, we can proceed to find the sample variance:

Sample Variance

We need to find the mean of the data as follows:

`\bar{x}=\frac{(7+9+14+16+18+22+23)_{}}{7}=(109)/(7)=15.5714285714`

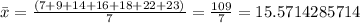
Now, we need to find the following sum:

`(7-\bar{x})^2+(9-\bar{x})^2+(14-\bar{x})^2+(16-\bar{x})^2+(18-\bar{x})^2+(22-\bar{x})^2+(23-\bar{x})`

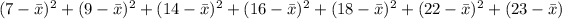
When calculating these statistics is good to round the value of the final result.

However, we were told to "round non-integer results to the nearest tenth". We will use the value of x (bar) (mean) as:

`\bar{x}=15.5714285714`

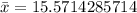
If we round this value to the nearest tenth, we will have a different result, but it is easier to work with:

`\bar{x}=15.6`

If we use mean = 109/7, the sum is:

`(7-(109)/(7))^2+(9-(109)/(7))^2+(14-(109)/(7))^2+(16-(109)/(7))^2+(18-(109)/(7))^2+(22-(109)/(7))^2+(23-(109)/(7))^2_{}`

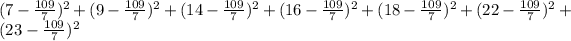
Then, the value is 221.714285714.

Now the value for the sample variance is:

`(Sx)^2=(1)/(n-1)\sum ^n_{i\mathop{=}1}(x_i-\bar{x})^2=(1)/(7-1)(221.714285714)=(1)/(6)(221.714285714)`
`(1)/(6)(221.714285714)=36.9523809523`

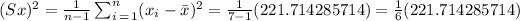
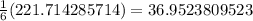
If we round the sample variance to the nearest tenth, we have that the value for the sample variance is 37.

Sample Standard Deviation

We know that the sample standard deviation is the square root of the sample variance. Then, we need to find the square root as follows:

`SD_{\text{sample}}=\sqrt[]{36.9523809523}=6.07884700846`

If we round the result to the nearest tenth, we have that the standard deviation is equal to 6.1.

In summary, we have that the range, the standard deviation, and the variance for given sample 7, 9, 14, 16, 18, 22, 23 are (rounded to the nearest tenth):

• Range = 16

,

• Standard deviation = 6.1

,

• Variance = 37