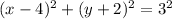Question

Find the standard form of the equation of a circle Center (4,-2) and tangent to the line x=1

Answer 1

According to the given data we have the following:

circle Center (4,-2)

tangent to the line x=1

To finde the standard form of the equation we would have to make the following:

According to the data the center is (h,k)=(4,-2)

using the following formula we can find the equation:

`(x-h)^2+(y-k)^2=r^2`

Since the tangent line is x=1 and r=4-1=3

Therefore, the standard form of the equation of a circle

Center (4,-2) and tangent to the line x=1 would be the following:

`(x-4)^2+(y+2)^2=3^2`