Question

Kobe Bryant and Lebron James are having a three point shooting competition. For each shot made, the player earns three points. For each shot missed, the player loses five points. After 40 Shots, Kobe has no points. How many shots did Kobe makes?1. define the variables2. write a system3. solve the system

Answer 1

Kobe made 25 shots

Step-by-step explanation

Step 1

Let x represents the number of shot made

Let y represents the number of shot loses

total points = 0

Hence,

For each shot made, the player earns three points. For each shot missed, the player loses five points

total points= 3x-5y

so

`\begin{gathered} 0=3x-5y\text{ Equation(1) } \\ \end{gathered}`

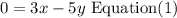
Also, the total shots is 40, so

`x+y=40\text{ Equation(2)}`

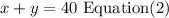
Step 2

write and solve the system

`\begin{gathered} 0=3x-5y \\ x+y=40 \end{gathered}`

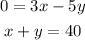
isolate x in equation (2) and replace in equation(1)

`\begin{gathered} x+y=40\text{ Equation(2)} \\ x=40-y\text{ Equation(3)} \\ \text{replace in Eq(1)} \\ 0=3x-5y\text{ Equation(1) } \\ 0=3(40-y)-5y\text{ } \\ 0=120-3y-5y \\ 0=120-8y \\ \text{subtract 120 in both sides} \\ 0-120=120-8y-120 \\ -120=-8y \\ \text{divide both sides by -8} \\ (-120)/(-8)=(-8y)/(-8) \\ 15=y \end{gathered}`

Step 3

replace the value of y in equation (3) to find x

`\begin{gathered} x=40-y\text{ Equation(3)} \\ x=40-15 \\ x=25 \end{gathered}`

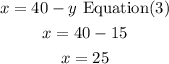
so,Kobie made 25 shots