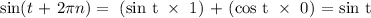Question

Use the identity sin(x+y)-sinxcosx to prove that sin(t+2pin)=sin t, for any integer n and any real number t.

Answer 1

`\sin (t\text{ + 2}\pi n)\text{ = sin t}`

Step-by-step explanation:

Here, we want to use identity to prove a given identity

Using the identity, we have it that:

`\text{ sin(t + 2}\pi n)\text{ = sint cos2}\pi n\text{ + cost sin2}\pi n`

We have it that cos 2pi equals 1 and sin 2pi equals zero

for n integer value that n might be, the product sin 2pi n will evaluate to zero and the product cos 2pi n will evaluate to zero

Thus, we have the evaluation as:

`\sin (t\text{ + 2}\pi n)=\text{ (sin t }*\text{ 1) + (cos t }*\text{ 0) = sin t}`