Question

As a copper wire is heated, its length increases by 0.100%. What is the change of thetemperature of the wire? (α = 16.6 × 10^−6/C°)a. 120.4°Cb. 60.2°Cc. 30.1°Cd. 6.0°C

Answer 1

Given:

Rate of increase of copper wire = 0.100%

Linear thermal expansion coefficient for Copper, α = 16.6 × 10^−6/C°

Let's find the change of the temperature of the wire.

To find the change in temperature of the wire, apply the formula:

`(\Delta l)/(l)=\alpha\Delta T`

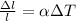
Where:

• ΔL/L is the rate of increase = 0.100% = 0.001

,

• α is the linear thermal expansion coefficient of copper = 16.6 × 10^−6/C°

,

• ΔT is the change in temperature.

Let's solve for ΔT.

We have:

`\begin{gathered} 0.001=16.6*10^(-6)\Delta T \\ \\ \Delta T=(0.001)/(16.6*10^(-6)) \\ \\ \Delta T=60.2^oC \end{gathered}`

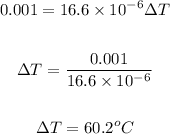
Therefore, the change of temperature of the wire is 60.2°C.

ANSWER:

b. 60.2°C