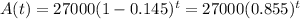Question

This is growth and decay problems. A population of 300 decreases by 8% each year. A $27000 car depreciates 14.5% each year. The formula is A(t) = a(1 + r)^t

Answer 1

We have two cases in which we need to write the formula for exponential growth or exponential decay, and we have the following two cases:

• A population of 300 decreases by 8% each year.

,

• A $27000 car depreciates 14.5% each year.

1. We can see that we have two cases of exponential decay, and the general formula in both cases is as follows:

`\begin{gathered} y=a(1-r)^x \\ \\ \text{ Which is equivalent to:} \\ \\ A(t)=a(1-r)^t \end{gathered}`

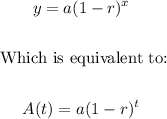
Where:

• a is the initial value (that is, the amount before starting the decay).

,

• r is the decay rate (the decay rate is given as a percentage, and we can express it as a decimal)

,

• t is the number of time intervals that have passed

2. And we can analyze both cases as follows:

First Case: A population of 300 decreases by 8% each year.

• The initial value, a = 300 (the initial population)

• The decay rate is 8% or we can express it as follows:

`r=8\%=(8)/(100)=0.08`

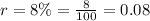
Now, we can express the scenario as follows:

`\begin{gathered} A(t)=300(1-0.08)^t=300(0.92)^t \\ \\ A(t)=300(0.92)^t \end{gathered}`

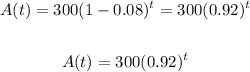
Second Case: A $27000 car depreciates 14.5% each year

We can proceed as before, and we have:

• a = $27000

• r = 14.5% which is equivalent to:

`\begin{gathered} r=14.5\%=(14.5)/(100)=0.145 \\ \\ r=0.145 \end{gathered}`

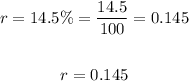
Therefore, we can express the situation as follows:

`\begin{gathered} A(t)=27000(1-0.145)^t \\ \\ A(t)=27000(0.855)^t \\ \end{gathered}`

Therefore, in summary, we can express both situations as follows:

• A population of 300 decreases by 8% each year:

`A(t)=300(1-0.08)^(t)=300(0.92)^(t)`

• A $27000 car depreciates 14.5% each year:

`A(t)=27000(1-0.145)^t=27000(0.855)^t`