ANSWER:
The mirror’s magnification is 0.06
The focal length is equal to 19.15 cm.
The mirror's radius of curvature is 38.3 cm
Explanation:
Given:
height image = 9 cm
height object = 1.5 m = 150 cm
The mirror's magnification is calculated using the following formula:
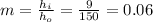
The mirror’s magnification is 0.06
Since we know the distance of the object which is -3 m (-300 cm) and the mirror's magnification we can calculate the distance of the image, just like this:
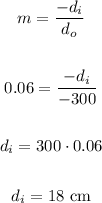
We calculate the focal length using the following formula:
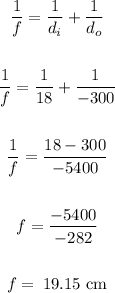
The focal length is equal to 19.15 cm.
Finally we calculate the mirror's radius of curvature knowing that twice the focal length, therefore:
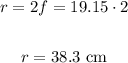
The mirror's radius of curvature is 38.3 cm