hello
the question talks about two supplementary angles. Now supplementary angles are two angles that their sum is equal to 180 degrees or basically angles of a straight line
this is an illustration of the angles
now we can proceed to solve for x by ading the sum and equating it to 180
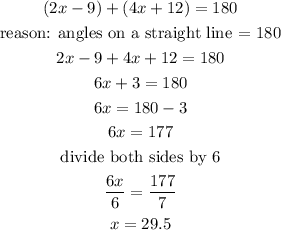
now that we've found the value of x, we can substitute it into the expression
1. 2x - 9
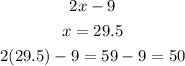
2. 4x + 12

the angles are 50 and 130 degrees respectively.
we can test if our answer is right by simply adding the two angles and if it gives exactly 180 degrees, then it's supplementary angle
50 + 130 = 180