Question

While Shopping Margaret bought a total of 10 items ( pants and t shirts) each pair of pants cost $53, each shirt is $27. She spent $374. How many pants and How many shirts.

Answer 1

Given that she bought a total of 10 items ( pants and t-shirts) each pair of pants cost $53, each shirt is $27. She spent $374, we have two linear equations as follows:

Let x be the number of pants and let y be the number of t-shirts, then:

`53x+27y=374`
`x+y=10`

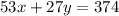
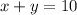
In order to find how many and shirts she bought, we have to solve this linear system of two equations and two variables:

`53x+27y=374\rightarrow53x=374-27y\rightarrow x=(374-27y)/(53)`
`\mathrm{Substitut}e\mathrm{\:}x=(374-27y)/(53)\text{ }into\text{ x + y = 10}`
`(374-27y)/(53)+y=10`
`(374+26y)/(53)=10`
`\mathrm{Isolate}\:y`
`(53\left(374+26y\right))/(53)=10\cdot \:53`
`374+26y=530`
`374+26y-374=530-374\rightarrow26y=156\rightarrow y=6`

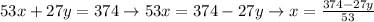
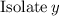
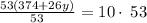
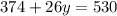
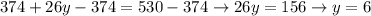
then:

`x=10-y=10-6=4`

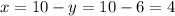
So, she bought 4 pants and 6 t-shirts.