Question

Graph the system of linear inequalities and shade in the solution set. If there are no solutions, graph the corresponding lines and do not shade in any region. 2x + y > 1 Y = greater and equal to 1

Answer 1

`\begin{gathered} 2x+y>1 \\ y\ge1 \end{gathered}`

To graph the given system of inequalities first draw the boundary lines of each one:

`\begin{gathered} 2x+y=1 \\ \\ y=1 \end{gathered}`

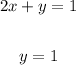
First inequality:

Find two points (x,y) using the first equation to draw the corresponding line:

When x=0

`\begin{gathered} 2(0)+y=1 \\ y=1 \\ \\ \text{Point: (0,1)} \end{gathered}`

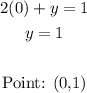
When x=2

`\begin{gathered} 2(2)+y=1 \\ 4+y=1 \\ y=1-4 \\ y=-3 \\ \\ \text{Point: (2,-3)} \end{gathered}`

As the inequality sing is > the line is a dotted line that passes trought points (0,1) and (2,-3)

Second inequality:

A line y=a is a horizontal line in y=a.

As the inequality sing is greater than or equal to the line is a full line in y=1

To find the solution you need to shadow the corresponding area for each inequality and if there is a area shaded by both inequalities it represents the solution:

First inequality: as the inequality sing is > the shaded area is above the boundary line (2x+y=1).

Second inequality: as the inequality sing is greater than or equal to the shaded area is above the boundary line (y=1)

Then, the graph of the system is:

First inequality in red

Second inequality in black

Solution: Area shaded by both inequalities