Question

On a piece of paper graph y

Answer 1

To answer this question, we need to follow the next steps.

1. This is an inequality, and there is a line that we need to represent it.

2. The line is y = x - 1.

3. We need to graph the line. For this, we can graph it using the x- and the y-intercept of the line.

[The x-intercept is the point where the line passes through the x-axis, and it is represented as (a, 0) - see that the value for y = 0. Likewise, the y-intercept is the point where the line passes through the y-axis, (0, b) - see that the value for x at this point is x = 0.]

4. Finding the x- and the y-intercepts:

Finding the x-intercept

`y=x-1\Rightarrow0=x-1\Rightarrow x=1`

Therefore, the x-intercept is (1, 0).

Finding the y-intercept

`y=x-1\Rightarrow x=0\Rightarrow y=0-1\Rightarrow y=-1`

Therefore, the y-intercept is (0, -1).

5. Finding the line equation

With these two points, (1, 0) and (0, -1), we need to label these points so we can apply the two-point form of the line as follows:

(1, 0) ---> x1 = 1, y1 = 0.

(0, -1) ---> x2 = 0, y2 = -1.

The two-point form of the line is given by:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

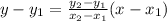
Substituting the corresponding values for x1, y1, x2, and y2, we have:

`y-0=(-1-0)/(0-1)(x-1)\Rightarrow y=(-1)/(-1)(x-1)\Rightarrow y=x-1`

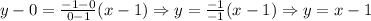
We were able to prove that the values are correct since we found the same line equation. Therefore, with those two points, we can graph the line.

6. Reference point to graph the inequality

Now, we need to use a reference point to see where the shaded area corresponding to the inequality is. We can choose the reference point (0, 0).

If we substitute the corresponding values for x = 0, and y = 0 in the inequality, we have:

[tex]yThe previous result is NOT TRUE: 0 is greater than -1. Therefore, the inequality must be in the other part of the line, and not the point (0,0) is. Additionally, we have that the values must be less than, <, which means the line must be graph as a dotted line.

Thus, we can graph the inequality as follows:

In summary, we can see above the graph of the inequality y < x - 1. We needed to find the x- and y-intercepts to find the line. After testing the reference point (0,0), we realized that the shaded area that corresponds to the inequality must be on the other side of the line - the other side of the line where the point (0, 0) is not. We needed to graph a dotted line since the values must be less, <, - and not equal to, in the inequality.