Question

Hi I need help please :). Directions: For each real world situation write and solve a system of equations give the solution as either an ordered pair or list what each variable is worth then explain what the solution means in terms of the situation

Answer 1

From the information in the statement, we know that

• 3 tickets and 2 combos cost $44

,

• 6 tickets and 5 combos cost $97.25

Then, let be

• x: the cost of a ticket

,

• y: the cost of a combo

And we can write the following system of linear equations

`\begin{cases}3x+2y=44\Rightarrow\text{ Equation 1} \\ 6x+5y=97.25\Rightarrow\text{ Equation 2}\end{cases}`

To solve the system of linear equations, we can use the elimination or reduction method.

First, we multiply Equation 1 by -2

`\begin{gathered} (3x+2y)\cdot-2=44\cdot-2 \\ \text{ Apply the distributive property to the left side of the equation} \\ 3x\cdot-2+2y\cdot-2=-88 \\ -6x-4y=-88 \end{gathered}`

Second, we add Equations 1 and 2

`\begin{gathered} -6x-4y=-88 \\ 6x+5y=97.25\text{ +} \\ ------------ \\ 0x+y=9.3 \\ \mathbf{y=9.3} \end{gathered}`

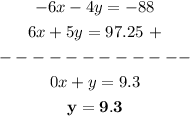
Third, since we already have the value of y, then we replace its value with any of the initial equations and solve for x. For example in Equation 1

`\begin{gathered} 3x+2y=44 \\ 3x+2(9.3)=44 \\ 3x+18.6=44 \\ \text{ Subtract 18.6 from both sides of the equation} \\ 3x+18.6-18.6=44-18.6 \\ 3x=25.4 \\ \text{ Divide by 3 from both sides of the equation} \\ (3x)/(3)=(25.4)/(3) \\ \mathbf{x=8.5} \end{gathered}`

Then, the solution of the system of linear equations that describes the situation mentioned in the statement is

`\begin{cases}x=8.5 \\ y=9.3\end{cases}`

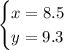
Finally, now we know that the cost of a ticket is $8.5 and that the cost of a popcorn/drink combo is $9.3.