Question

The function F(x)=x^3 +2 is one to one Find A & B

Answer 1

Considering the function

`f(x)=x^3+2`

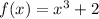
To determine the inverse function, first, replace f(x) for y to make the calculations simpler:

`\begin{gathered} f(x)=x^3+2 \\ y=x^3+2 \end{gathered}`

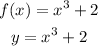
Next, write the expression for y:

- Subtract 2 to both sides of the expression:

`\begin{gathered} y-2=x^3+2-2 \\ y-2=x^3 \end{gathered}`

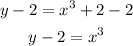
- Apply the cubic root to both sides of the equal sign:

`\begin{gathered} \sqrt[3]{y-2}=\sqrt[3]{x^3} \\ x=\sqrt[3]{y-2} \end{gathered}`

Since the variables are assigned arbitrarily, you can change y for x:

`y=\sqrt[3]{x-2}`

And use function notation:

`f(x)^(-1)=\sqrt[3]{x-2}`

The domain for the inverse function is all values of x, since odd powers, such as this one can be negative and positive.

The correct option is C.

b) Calculate f(f⁻¹(x)), first, write f(x) when x=f⁻¹(x), then simplify:

`\begin{gathered} f(x)=x^3+2 \\ f(f(x)^(-1)))=(\sqrt[3]{x-2})^3+2 \\ f(f(x)^(-1)))=x-2+2 \\ f(f(x)^(-1)))=x \end{gathered}`

Calculate f⁻¹(f(x)), write f⁻¹(x) when x=f(x)

`\begin{gathered} f^(-)^(1)\mleft(x\mright)=\sqrt[3]{x-2} \\ f^(-)^(1)\mleft(f(x)\mright)=\sqrt[3]{(x^3+2)-2} \end{gathered}`

Erase the parentheses and simplify:

`\begin{gathered} f^(-)^(1)\mleft(f(x)\mright)=\sqrt[3]{x^3+2-2} \\ f^(-)^(1)(f(x))=\sqrt[3]{x^3} \\ f^(-)^(1)(f(x))=x \end{gathered}`