Question

I'll show you a picture of the problem because it's complicated

Answer 1

We are given two options diagrams A and B and we are required to use choose either A or B for which option properly represents the scenario presented in the sub-questions of Question 3.

Question 3.1:

The amount of rain this year decreased by 10% compared to last year. This implies that if last year's amount of rain was X, then this year's rain has decreased by 10% of X. Mathematically, we have:

`\begin{gathered} \text{Last year's rain=X} \\ \text{The decrease in year's rain=}(10)/(100)* X=0.1X \\ \\ \therefore\text{This year's rain = X}-0.1X=0.9X \end{gathered}`

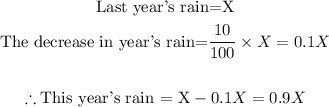
This means that last year's rain must be 100% while this year's rain has a 10% decrease in the rainfall.

The option that depicts this properly is OPTION A

Question 3.2:

The amount of sleet this year is 90% of last year's amount. This implies that if last year's amount of sleet is X, then this year's sleet amount must be 90% of X. That is:

`\begin{gathered} Last\text{ year}=X \\ \text{This year}=(90)/(100)* X=0.9X \\ \\ \text{Thus, the change in sleet from last year to this year is:} \\ X-0.9X=0.1X \end{gathered}`

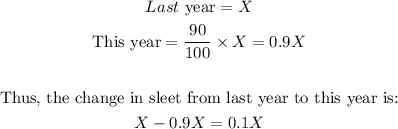
This means that Last year's amount is again 100% while this year is 10% less than last year.

The option that depicts this properly is OPTION A

Question 3.3:

The amount of sunshine this year increased by 10% compared with last year's amount. This implies that if last year's sunshine is X and then this year's sunshine must be 10% greater than X. That is:

`\begin{gathered} \text{Last year}=X \\ \text{ Increase }=(10)/(100)* X=0.1X \\ \\ \therefore\text{This year}=Last\text{ year }+Increase \\ \text{This year}=X+0.1X=1.1X \end{gathered}`

This means that last year's amount is 100% while this year's amount is 10% greater.

The option that depicts this properly is OPTION B.

Question 3.4:

The number of windy days this year is 110% of last year's number. This implies that this year's number has increased by 10% given that last year's number was 100%.

The option that depicts this property is OPTION B

Question 3.5:

The percentage change in Graph A is:

`\begin{gathered} \text{ \% change }=\text{ This year's amount - Last year's amount} \\ \text{ \% change }=-10\text{ \% (from the diagram)} \end{gathered}`

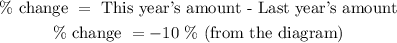
The answer is -10%

(Note: This is negative because it is a decrease from last year to this year)

Question 3.6:

The percentage change in Graph B is:

`\begin{gathered} \text{ \%change}=\text{ This year's amount }-\text{ Last year's amount} \\ \text{ \%change}=10\text{ \% (from the diagram)} \end{gathered}`

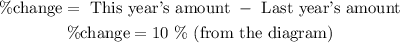
The answer is 10%

Final Answer

Question 3.1:

OPTION A

Question 3.2:

OPTION A

Question 3.3:

OPTION B

Question 3.4:

OPTION B

Question 3.5:

The answer is -10%

Question 3.6:

The answer is 10%