expressionGiven from the original,
Volume=V; radius= r and height = 12cm
Please note that the volume V, of a cone, is calculated with the formula
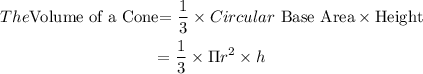
For question (a)
height is the same as the original but the radius is
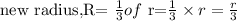
The expression for the new volume will give us
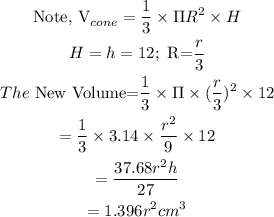
(a) Therefore, The expression for the new volume is 1.396r²cm³
(b) At this time, the height has the height as the original cone but 3 times the radius of the original cone.
Note that the new height still remains as h, while the new radius will be
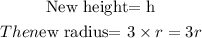
Substituting the new height and the new radius into the formula for the volume of the cone will give
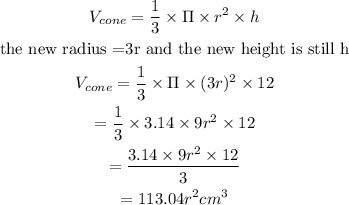
(b) Therefore, the expression for the new volume is 113.04r²cm³