Explanation
We are given the following:
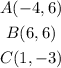
We are required to determine whether or not triangle ABC is an equilateral triangle.
We know that an equilateral triangle is a triangle with all sides equal.
We also know that the distance between two points is given as:
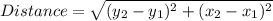
- The distance AB becomes:
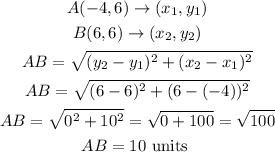
- The distance BC becomes:
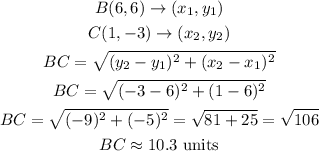
Hence, the answer is:
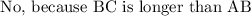
Option C is correct.