Given: The equation a circle below
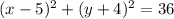
To Determine: The center and the radius
Solution
The general equation a circle given the center and the radius is
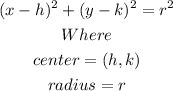
Compare the given to the general equation to get the center and radius
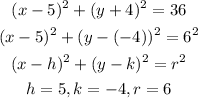
Hence, the center is (5, - 4), and radius is 6 units