Question

you are on vacation in new York city, and you need to get around town to different locations. below are the rates for 2 different cab companies, locally dubbed "the red cabs" and "the green cabs" questions :1 - what is the cost to get into a red cab?2 - how much does it cost per mile for a red cab? 3 - what is the equation, in slope-intercept form, that relates the cost compared to the miles traveled for a red cab ?

Answer 1

The solution to the questions is obtained from the interpretation of the graph.

Consider the image of the graph given

From the diagram above, the cost to get into a red cab is when the miles is at zero which is the y-intercept

From the graph above, the cost of getting into a red cab is

`\begin{gathered} \text{ \$2} \\ \text{The y-intecept of the red line} \end{gathered}`

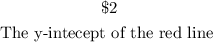
Hence

1). The cost to get into a red cab is $ 2

For the red cab, we use the red line

`\text{The cost per unit mile is the slope of the red line}`

The slope of the red line is obtained by

`\begin{gathered} \text{Slope= }\frac{\text{Changes in Cost}}{Changes\text{ in miles }} \\ \\ \text{Slope =}\frac{\text{4-2}}{1-0}=(2)/(1)=2 \\ \text{Cost per mile is \$2/miles} \end{gathered}`

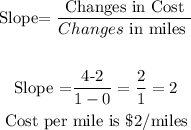
Hence

2). The cost per mile for a red cab is $2 per mile

The equation of the line in slope and intercept form is given by

`\begin{gathered} C=mt+b \\ \text{Where} \\ C\text{ is the cost , t is the miles } \\ m=\text{slope the cost per mile } \\ b=\text{intercept on the y i.e cost of geting into the red cab } \end{gathered}`

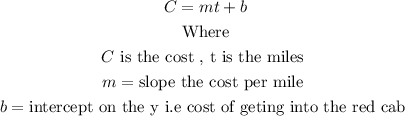
Since

`\begin{gathered} m=2 \\ \text{and } \\ b=2 \end{gathered}`

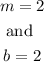
Then, the required equation is

`C=2t+2`

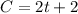
Therefore

3). The equation in slope-intercept form that relates the cost to the miles travelled for a red carb is C = 2t + 2