To find the answer, we will need to replace the population P by 50,000 and solve the initial equation for t because t is the number of years after 2012.
So, we get:
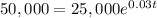
Now, we need to remember some properties of the logarithms:
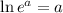
Then, we can solve for t as:

So, using the property, we get:
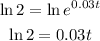
Finally, dividing by 0.03 into both sides, we get that the number of years after 2012 that the population will be 50,000 is:
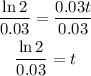
Answer: t = ln2/0.03