Question

It took Eric 11 hours to drive to a family reunion. On the way home, he was able to increase his average speed by 18 mph and makethe return drive in only 8 hours. Find his average speed on the return drive.Step 1 of 3: Complete the following table by entering the missing values, using x to represent the unknown quantity.

Answer 1

The Solution:

Given the initial values as below:

`\begin{gathered} \text{Let the original speed/ rate be x} \\ \text{Time(t)}=11\text{ hours} \\ So,\text{ we have the distance(d) to be:} \\ d=x*11=11x\ldots eqn(1) \end{gathered}`

The average speed was increased by 18m/h and a return time of 8 hours only.

`\begin{gathered} \text{ speed(s)=(x+18) m/h} \\ \text{ Time(t)=8 hrs} \\ So, \\ d=(x+18)(8)=8x+144\ldots eqn(2) \end{gathered}`

Equating both eqn(1) and eqn(2), we get

`\begin{gathered} 11x=8x+144 \\ 11x-8x=144 \\ 3x=144 \\ \text{Dividing both sides by 3} \\ (3x)/(3)=(144)/(3) \\ \\ x=48\text{ m/h} \end{gathered}`

The distance is

`d=11x=11*48=528m`

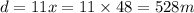
Thus, the average speed on his return drive is:

`\text{ Average speed=x}+18=48+18=66\text{ m/h}`

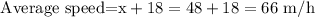
Therefore, the correct answer is 66 m/h

Original values:

x=48m/h

t=11 hrs

d=528m

Return Drive:

x=66m/h

t=8 hrs

d=528m