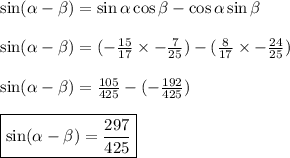Given
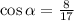
,
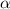
is in Quadrant IV,

, and

is in Quadrant III, find
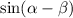
We can use the angle subtraction formula of sine to answer this question.
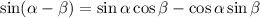
We already know that
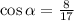
.
We can use the Pythagorean identity

to find
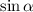
.

Since
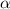
is in Quadrant IV, and sine is represented as y value on the unit circle, we must assume the negative value
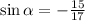
.
As similar process is then done with

.
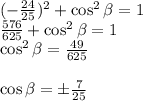
And since

is in Quadrant III, and cosine in represented as x value on the unit cercle, we must assume the negative value
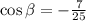
.
Now we can fill in our angle subtraction formula!