Question

2. Solve for x(1/3)(5+7x) = 12 - (1/2)(3-2x)

Answer 1

To solve the equation below:

`(1)/(3)(5+7x)=12-(1)/(2)(3-2x)`

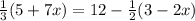
eliminate the denominators by multiplying each term on both sides of the equation by the least common denominator or the LCD. In this case, since the least common multiple of 3 and 2 is 6, the LCD must be 6.

`\begin{gathered} 6\lbrack(1)/(3)(5+7x)\rbrack=6\lbrack12-(1)/(2)(3-2x)\rbrack \\ 6\lbrack(1)/(3)(5+7x)\rbrack=6\lbrack12\rbrack-6\lbrack(1)/(2)(3-2x)\rbrack \\ 2(5+7x)=72-3(3-2x) \end{gathered}`

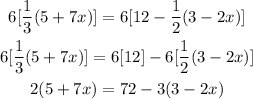
Eliminate the parentheses by distributing the numerical values outside the parentheses. In this case, we distribute the 2 to 5 and 7x and then distribute -3 to 3 and -2x.

`\begin{gathered} 2(5)+2(7x)=72-3(3)-3(-2x) \\ 10+14x=72-9+6x \end{gathered}`

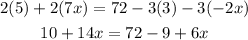
Simplify both sides of the equation by combining like terms. Like terms are the terms with the same literal coefficients.

`10+14x=63+6x`

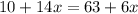
Isolate the variable terms by subtracting 6x and 10 from both sides of the equation.

`\begin{gathered} 10+14x-6x-10=63+6x-6x-10 \\ 8x=53 \end{gathered}`

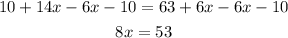
Solve for x by dividing both sides of the equation by 8.

`\begin{gathered} (8x)/(8)=(53)/(8) \\ x=(53)/(8) \end{gathered}`

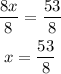
Therefore, the value of x must be 53/8.