Question

What is the inverse of f(x)=(x+6)2 for x≥–6 where function g is the inverse of function f? g(x)=x√−6,x≥0g(x)=x+6‾‾‾‾‾√,x≥−6g(x)=x−6‾‾‾‾‾√,x≥6g(x)=x√+6,x≥0

Answer 1

The inverse of f(x) is:

`g(x)=\sqrt[]{x}-6\text{ (OPTION 1)}`

Solution

The question asks us to find the inverse of the following function:

`f(x)=(x+6)^6`

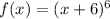
- For us to find the inverse of the function, we simply need to follow these steps:

1. Replace f(x) with y and make x the subject of the formula.

2. Substitute x for y and y for x in the expression gotten from step 1.

3. Replace y with g(x), which is the inverse of the function f(x)

- With the steps outlined above, we can proceed to solve the question:

Step 1

`\begin{gathered} f(x)=(x+6)^2 \\ \text{ Replace f(x) with y} \\ y=(x+6)^2 \\ \\ \text{Make x the subject of the formula} \\ \text{ Find the square root of both sides} \\ \sqrt[]{y}=x+6 \\ \\ \text{Subtract 6 from both sides} \\ x=\sqrt[]{y}-6 \end{gathered}`

Step 2:

`\begin{gathered} \text{The result from step 1 is:} \\ x=\sqrt[]{y}-6 \\ \\ \text{Exchange x for y and y for x} \\ y=\sqrt[]{x}-6 \end{gathered}`

Step 3:

`\begin{gathered} Th\text{e expression from step 2 is given by:} \\ y=\sqrt[]{x}-6\text{ } \\ \text{ Replace y with g(x)} \\ \\ \therefore g(x)=\sqrt[]{x}-6 \end{gathered}`

Final Answer

The inverse of the function f(x) is given by:

`g(x)=\sqrt[]{x}-6\text{ (OPTION 1)}`