a) 13.25 m
b)22.3 degrees
Step-by-step explanation
Step 1
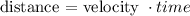
Let
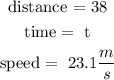
so
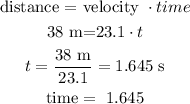
now , to find the disntace to the targe let's use the formula
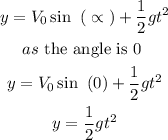
hence
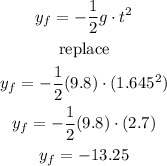
so,target missed by 13.25 meters.
Step 2
b)At what angle should the bow be aimed in order to hit the target?
to solve this we can use the expression
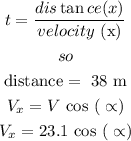
now, replace and solve for the angle

so, the angle should be
22.3 degrees