We are given that there are a total of 78 students. If we set the following variables:
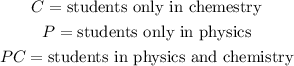
Then, the sum of all of these must be 78, that is:
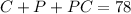
Since there are 15 in chemistry and physics and 47 in chemistry, we may replace that into the equation and we get:

Simplifying:
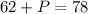
Now we solve for P by subtracting 62 on both sides:
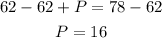
Therefore, there are 16 students in physics