Question

A metal measuring tape expands when the temperature goes above 50°F. For every degree Farenheit above 50, its length increases by 0.00064%.1. The temperature is 100 degrees Fahrenheit. How much longer is a 30-foot measuring tape than its correct length?2. What is the percent error?

Answer 1

1.

First, let's find a function that describes this situation.

Let:

t be the temperature of the measuring tape:

L(t) be the lengt of the tape

We'll have that:

`\begin{gathered} L(t)=30+(t-50)(30\cdot(0.00064)/(100)),t\ge50 \\ \end{gathered}`

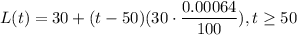
Let's calculate L(100):

`\begin{gathered} L(100)=30+(100-50)(30\cdot(0.00064)/(100)) \\ \rightarrow L(100)=30.0096 \end{gathered}`

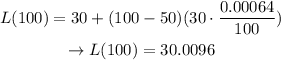
The tape is now 0.0096ft longer

2.

To get the percent error, we divide the original lenght by the expanded lenght, substract that from 1, and multiply by 100:

`(1-(30)/(30.0096))\cdot100\rightarrow0.03`

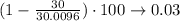
The percent error is 0.03%