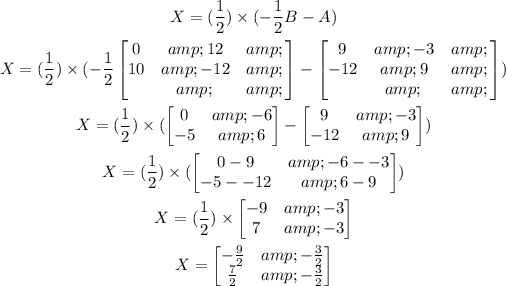Question

Given the matrices A and B shown below, solve for X in the equation2X + A=-B.A9-12-3793B=01012-12Rows: 2 0Columns: 2Submit Answernamnteconto

Answer 1

Let's solve for X in the matrix equation first,

`\begin{gathered} 2X+A=-(1)/(2)B \\ 2X=-(1)/(2)B-A \\ X=(-(1)/(2)B-A)/(2) \\ or, \\ X=((1)/(2))*(-(1)/(2)B-A) \end{gathered}`

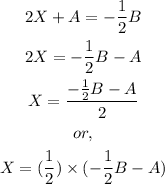
This means, we have to find (-1/2B) and then subtract A.

We then multiply that matrix by the scalar constant (1/2).

*Remember, multiplying a matrix by a scalar means multiplying all the entries of the matrix by that scalar.

* Also, when we subtract matrices, we are basically subtracting each corresponding entry from each other

Let's show the matrix operations:

`\begin{gathered} X=((1)/(2))*(-(1)/(2)B-A) \\ X=((1)/(2))*(-(1)/(2)\begin{bmatrix}{0} & {12} & {} \\ {10} & {-12} & {} \\ {} & {} & {}\end{bmatrix}-\begin{bmatrix}{9} & {-3} & {} \\ {-12} & {9} & {} \\ {} & {} & {}\end{bmatrix}) \\ X=((1)/(2))*(\begin{bmatrix}0 & -6 \\ -5 & 6\end{bmatrix}-\begin{bmatrix}9 & -3 \\ -12 & 9\end{bmatrix}) \\ X=((1)/(2))*(\begin{bmatrix}0-9 & -6--3 \\ -5--12 & 6-9\end{bmatrix}) \\ X=((1)/(2))*\begin{bmatrix}-9 & -3 \\ 7 & -3\end{bmatrix} \\ X=\begin{bmatrix}-(9)/(2) & -(3)/(2) \\ (7)/(2) & -(3)/(2)\end{bmatrix} \end{gathered}`