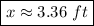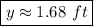Question

A normal window is constructed by adjoining a semicircle to the top of an ordinary rectangular window, (see figure ) The perimeter of the window is 12 feet. what dimensions will produce a window of maximum area? (Round you answers to two decimal places ) what is the width x= what is the length y.?

(Question2) write the function in the form f(×) = ×^3- 6×^2- 15×+9, k = -2.
f (×)=?

Answer 1

Let's find the perimeter of the window.

The bottom side is
`x`. The left and right sides make
`2y`.
The perimeter of a circle is
`2\pi r`, so the perimeter of a semicircle must be
`\pi r`, The radius is
`\frac{1}2x`, so that gives
`\frac{1}2\pi x` for the curve. All of that is equal to 12.


`x+2y+\frac{1}2\pi x=12`

We only want to use one variable to create the area formula, so let's solve for
`y`.


`2y=12-x-\frac{1}2\pi x`


`y=6-\frac{1}2x-\frac{1}4\pi x`

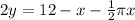
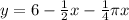
Now that we have a value for
`y` in terms of
`x`, we can find the area in terms of
`x`.

The area of the rectangle is going to be
`xy`, which then becomes


`A_r=x(6-\frac{1}2x-\frac{1}4\pi x`


`A_r=6x-\frac{1}2x^2-\frac{1}4\pi x^2`

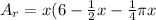
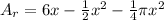
The area of the semicircle is going to be
`\frac{1}2\pi r^2`.

Since
`r=\frac{1}2x`,
`A_(sc)=\frac{1}2\pi (\frac{1}2x)^2`.


`A_(sc)=\frac{1}2\pi \frac{1}4x^2`


`A_(sc)=\frac{1}8\pi x^2`

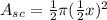
Now let's add the areas of the rectangle and semicircle.


`A=A_r+A_(sc)`


`A=6x-\frac{1}2x^2-\frac{1}4\pi x^2+\frac{1}8\pi x^2`


`A=6x-\frac{1}2x^2-\frac{1}8\pi x^2`

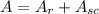
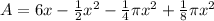
If you wanted to factor out
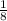
`\frac{1}8` like you did, this would become


`\boxed{A(x)=\frac{1}8(48x=4x^2-\pi x^2)}`

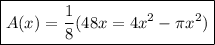
Now what we want to do is find what
`x` is when
`A` is at its highest point, Once we have the value for
`x` we can also find the value for
`y`, of course.

Let's put our equation in the general form of a quadratic.


`A(x)=(-\frac{1}2-\frac{1}8\pi )x^2+6x`

Now we can use the vertex formula
`x=(-b)/(2a)`.
(
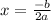
`a` and
`b` refer to
`ax^2+bx+c`.)


`x=\frac{-6}{2(-\frac{1}2-\frac{1}8\pi)}`


`x=\frac{-6}{-\frac{1}4\pi -1}`


`x=(-24)/(-\pi -4)`


`\boxed{x=(24)/(\pi +4)}`

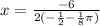
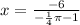
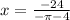
Now let's plug that in for
`y=6-\frac{1}2x-\frac{1}4\pi x`.

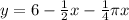
Since our final answers are in decimal form and not exact form, we can make our lives a little easier here and just use
`x\approx3.36059492`.


`y\approx6-\frac{1}2(3.36059492)-\frac{1}4\pi(3.36059492)`


`y\approx6-(1.68029746+2.63940507809)`


`\boxed{y\approx1.68029746191}`

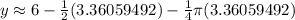
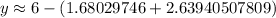
Let's take our answers for
`x` and
`y` and round to 2 decimal places.


`\boxed{x\approx 3.36\ ft}`


`\boxed{y\approx 1.68\ ft}`