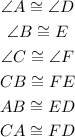To indicate congruence of angles, we draw a semicircle-like along the angle. As we can see on the figure, angle A and angle D has one semicircle, hence, they are congruent. Angles B and E are also congruent because they both have two semicircle. Lastly, angles C and F are congruent with the same reasoning.
To indicate congruence on the lengths of the sides of the triangle, we put a line along the side. Based on this reasoning, side AB and side ED are congruent since these sides have one line.
Side CB has two lines. But the other triangle doesn't have any side that has 2 sides. But we can see on triangle ACB that the side CB is along angles C and B. This is congruent to the side EF with angles E and F. Hence, side CB is congruent with side EF.
Lastly, we have side CA which is not evaluated yet. It lies between angles A and C. This is the same as the side FD that lies between angles F and D. Hence, side CA is congruent with side FD.
Answer: