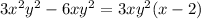From the binomial:
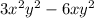
We can factor out the GCF by factoring out the GCF of the coefficients, and the lowest power of each variable.
The GCF of 3 and 6 is 3.
The lowest power of x is 1.
The lowest power of y is 2.
Then, we can factor out:
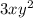
Multiply each term by:
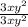
Which does not change the meaning of the expression, since that fraction is equal to 1:
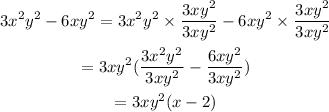
Therefore: