Given,
let C1 = 0.45 μF and C2 = 0.67 μF
And Voltage = 15 V.
Here both the capacitor are in series so the equivalent capacitor is,
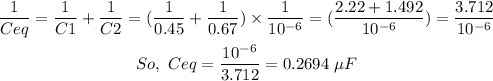
As we know that,
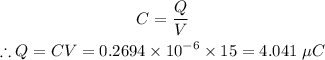
So charge on each capacitor will be equal to 4.041 μC.
The capacitors are connected in series so the charge on both the sphere will be same but potential difference across each capacitor will be different.
The voltage across the capacitors are,
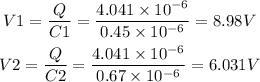
So potential difference across C1 is 8.98V and C2 is 6.031V.
If we connect both the capacitor in parallel connection then the equivalent capacitor will be,
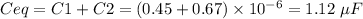
In parallel connection the voltage across the capacitor will be same but the charge will be different.
So the potential across each capacitor is 15 Volt.
The charge on each capacitor is,
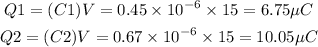
So in parallel connection the charge on C1 = 6.75 μC and charge on C2 = 10.05 μC.