Question

Suppose a square has sides of length 5. If we double the length of the sides, what is the ratio of the area of the new square to the area of the old square?A) 5:1B) 4:1C) 1:4D) 2:1

Answer 1

`B)\text{ }4:1`

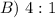
Step-by-step explanation

The length of the side of the square is 5.

If the length is doubled, it becomes:

`\begin{gathered} 5*2 \\ \\ 10 \end{gathered}`

The area of the square with a length of 5 is:

`\begin{gathered} A=L^2 \\ \\ A=5^2 \\ \\ A=25 \end{gathered}`

The area of the new square with a length of 10 is:

`\begin{gathered} A=10^2 \\ \\ A=100 \end{gathered}`

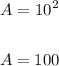
Hence, the ratio of the area of the new square to the area of the old square is:

`\begin{gathered} 100:25 \\ \\ 4:1 \end{gathered}`

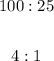
The answer is option B.