Question

For a particular event, 828 tickets were sold for a total of $6279. If students paid $6 per ticket and non-students paid $9 per ticket, how many student tickets were sold?

Answer 1

Out of the 828 tickets sold, some were student's tickets, while the rest were non-students tickets.

Let s represent student's tickets and n represent non-student tickets.

So that means s + n = 828 ......... equation 1

All the tickets were sold for $6279. Students' tickets sold for $6 and non-students' tickets sold for $9. This means that

6 x s + 9 x n = 6279

6s + 9n = 6279........... equation 2

So we will solve equations 1 and 2 simultaneously we have

`\begin{gathered} s+n=828 \\ 6s+9n=6279 \\ \\ (s+n=828)*9 \\ (6s+9n=6279)*1 \\ \\ 9s+9n=7452 \\ 6s+9n=6279 \\ \\ 9s+9n=7452 \\ (-)6s+9n=6279\text{ multiplying by (-) to eliminate 9n} \\ \\ 9s+9n=7452 \\ -6s-9n=-6279 \\ \\ 3s=1173 \\ s=\text{ }(1173)/(3) \\ \\ s=391 \end{gathered}`

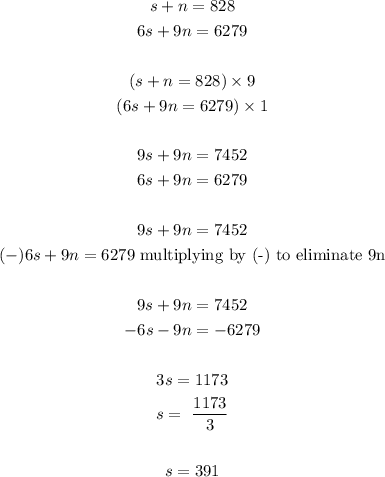
Therefore, the number of students tickets sold is 391