a) Future value is $17061.98
b)
Step-by-step explanation:
a) Principal = $10427
rate = 4.502% = 0.04502
time = 11 years
n = number of times compounded = quarterly
n = 4
FV = future value = ?
To get the future value, we will apply compound interest formula:
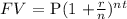
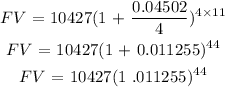
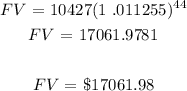
Future value is $17061.98
b) For continuous compounding, the formula is given by:
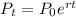
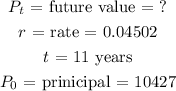
![undefined]()