Question

Suppose that there are two types of tickets to a show: advance and same-day. The combined cost of one advance ticketand one same-day ticket is $65. For one performance, 25 advance tickets and 30 same-day tickets were sold. The totalamount paid for the tickets was $1750. What was the price of each kind of ticket?Advance ticket: s[]Same-day ticket: s[]

Answer 1

Let's call a the price of advance tickets, and s the price of same-day tickets.

The combined price of one and one is $65. Then, we can establish the following equation:

`a+s=65`

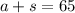
When 25 advance tickets and 30 same-day tickets were sold, the total amount paid for the tickets was $1750. Then, the sum of the total amount of money paid for advanced tickets (25a, the number of tickets paid multiplied by their price), and the total amount of money paid for the same-day tickets (30s, following the same logic), should add up to $1750. Representing that in an equation:

`25a+30s=1750`

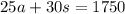
Now we have a system of two equations and two unknowns (the price for each kind of ticket).

We can solve the system by using the substitution method.

We can isolate one of the variables from the first equation, and then replace the expression on the second equation. Solving for s in the first equation:

`s=65-a`

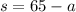
Now, we can replace that expression in the second equation instead of s:

`25a+30\cdot(65-a)=1750`

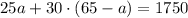
Now we have one equation with only one unknown. We can easily solve now the value of a:

`\begin{gathered} 25a+30\cdot65-30a=1750 \\ 25a-30a=1750-30\cdot65 \\ -5a=1750-1950 \\ a=(-200)/(-5) \\ a=40 \end{gathered}`

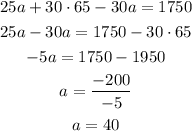
Then, the price of the advance ticket is $40.

Recalling that the combined price of one ticket of each class is $65:

`a+s=65`

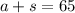
Replacing the price of the advance ticket and solving:

`\begin{gathered} 40+s=65 \\ s=65-40 \\ s=25 \end{gathered}`

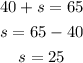
The price of the same-day tickets is $25