Question

Find the coordinates of P so that P partitions segment A to B in the ratio 5:1 with A(2,

4) and B(8, 10).

Answer 1

Point P has coordinates (7,9) (last choice)

Explanation:

We are given the endpoints A(2,4) B(8,10) and the point P lying on the segment AB with the condition that P partitions it in the ratio 5:1.

This means the distances AP, PB and AB follow the conditions:

`(AP)/(PB)=(5)/(1)`

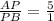
AP+PB=AB

We can work with each coordinate separately. Suppose P has coordinates (x,y), thus:

`x-x_a=5(x_b-x)`

`x-x_a=5x_b-5x`

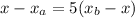
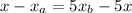
Adding 5x and subtracting:

`6x=5x_b+x_a`

Dividing by 6:

`\displaystyle x=(5x_b+x_a)/(6)`

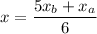
Substituting:

`\displaystyle x=(5*8+2)/(6)=(42)/(6)=7`

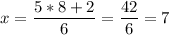
x=7

Now for the y-axis:

`\displaystyle y=(5y_b+y_a)/(6)`

Substituting:

`\displaystyle y=(5*10+4)/(6)=(54)/(6)=9`

y=9

Point P has coordinates (7,9) (last choice)