The probability of getting P(greater than 2 or less than 4) is given by
![\begin{gathered} P(\text{greater than 2 OR less than 4)=P(greater than 2)}+P(\text{less than 4)-P(greater than 2 AND less than 4)} \\ \text{which is equal to} \\ P(\text{greater than 2 OR less than 4)=P(greater than 2)}+P(\text{less than 4)-P(3)} \end{gathered}]()
because the a number greater than 2 and less than 4 is 3.
Since the cube has 6 faces, the probability of getting one face is 1/6, then we have

Similarly,
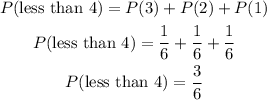
since P(3)= 1/6, we have
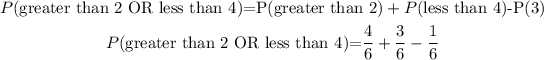
which gives
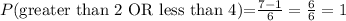
Therefore, the answer is 1.