Question

Select the correct choice below and fill in any answer boxes in your choice.

Answer 1

The given equation is

`x(5x-5)=(5x+9)(x-4)`

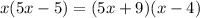
We will simplify each side at first by multiply the brackets on the right side and multiply the common factor by the bracket on the left side

`\begin{gathered} x(5x)-x(5)=(5x)(x)+5x(-4)+(9)(x)+(9)(-4) \\ 5x^2-5x=5x^2-20x+9x-36 \end{gathered}`

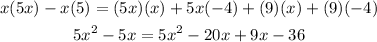
Now, we will add the like terms on each side

`\begin{gathered} 5x^2-5x=5x^2+(-20x+9x)-36 \\ 5x^2-5x=5x^2-11x-36 \end{gathered}`

Subtract both sides by 5x^2

`\begin{gathered} 5x^2-5x^2-5x=5x^2-5x^2-11x-36 \\ -5x=-11x-36 \end{gathered}`

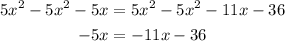
Add 11x to both sides

`\begin{gathered} -5x+11x=-11x+11x-36 \\ 6x=-36 \end{gathered}`

Divide both sides by 6

`\begin{gathered} (6x)/(6)=-(36)/(6) \\ x=-6 \end{gathered}`

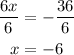
The solution set is {-6}

The answer is A